Sembla una pregunta senzilla: perquè només en veiem la part il·luminada pel sol, i perquè la posició relativa entre el sol i la lluna va canviant al llarg de tot el cicle lunar de 29 dies.

Fa uns 2300 anys, a Alexandria, Aristarc de Samos va pensar el mateix. Però va anar més enllà, i com a bon científic, va veure i va saber interpretar el que tothom tenia davant dels seus ulls però no comprenia. Aristarc es va situar mentalment a la lluna, en el moment del quart creixent. Si des de la terra veiem exactament la meitat de la lluna il·luminada i la meitat no, és que estem mirant “de costat”. És el mateix que quan fem una foto a una persona. Si el sol és baix (per exemple, a punt de pondre’s) i fem la foto amb el sol de costat, a la foto veurem mitja cara rebent la llum del sol i mitja cara a l’ombra. El raonament d’Aristarc va ser impecable. Va començar pensant que a l’espai, la terra, la lluna i el sol formaven un triangle. En el moment del quart creixent, la lluna té el sol de costat. Per tant, el triangle terra-lluna-sol en aquest moment ha de ser rectangle. En altres paraules, l’angle (mesurat des de la lluna i en el moment del quart creixent) entre el sol i la terra, ha de ser de noranta graus. És admirable, no? Simplement mirant la lluna des de la terra, Aristarc va deduir l’angle que hauria vist si hagués anat a la lluna!

Aristarc  va ser probablement el primer en continuar el raonament i deduir que el sol era molt més lluny que la lluna. Ho va fer connectant idees, barrejant la seva abstracció del triangle rectangle lluna-terra-sol amb les eines de càlcul geomètric i trigonomètric que existien llavors. Simplement, i des d’Alexandria, va mesurar l’angle entre la lluna i el sol en el moment del quart creixent i amb això va poder saber el valor dels tres angles del triangle rectangle lluna-terra-sol. Va concloure que el sol era unes 18 vegades més lluny que la lluna.

No sabem si aquesta deducció la va fer Aristarc per primer cop, o si es va inspirar en texts i treballs d’astrònoms anteriors. En sabem molt poc, dels avenços i dels descobriments dels antics. Però el que sí és clar és que fa 2300 anys ja hi havia qui sabia com calcular distàncies relatives entre la terra, la lluna i el sol.

L’únic problema que va tenir Aristarc va ser un problema de mesura. Els seus instruments eren precaris, i es va equivocar quan va mesurar l’angle entre la lluna i el sol. Si intenteu repetir el seu experiment (ho haureu de fer al matí, que és quan, a la fase de quart creixent, podem veure simultàniament la lluna i el sol al cel), comprovareu que l’angle entre la lluna i el sol és quasi de noranta graus. De fet, és de 89 graus i 51 minuts. La seva mesura, en canvi, va ser d’uns 87 graus. El seu raonament va ser totalment correcte, però no va poder mesurar millor l’angle. Ara sabem que un error de quasi tres graus en un triangle rectangle tant allargat produeix errors molt grans en el resultat. De fet, el sol és bastant més lluny: uns 400 cops més lluny que la lluna.

Aristarc de Samos va defensar la teoria heliocèntrica, però no li van fer cas. Les teories geocèntriques, amb la terra al bell mig de l’univers, dominaven en el camp de l’astronomia. Van haver de passar quasi 1800 anys fins que Copèrnic ens va demostrar que no érem al centre de l’univers.

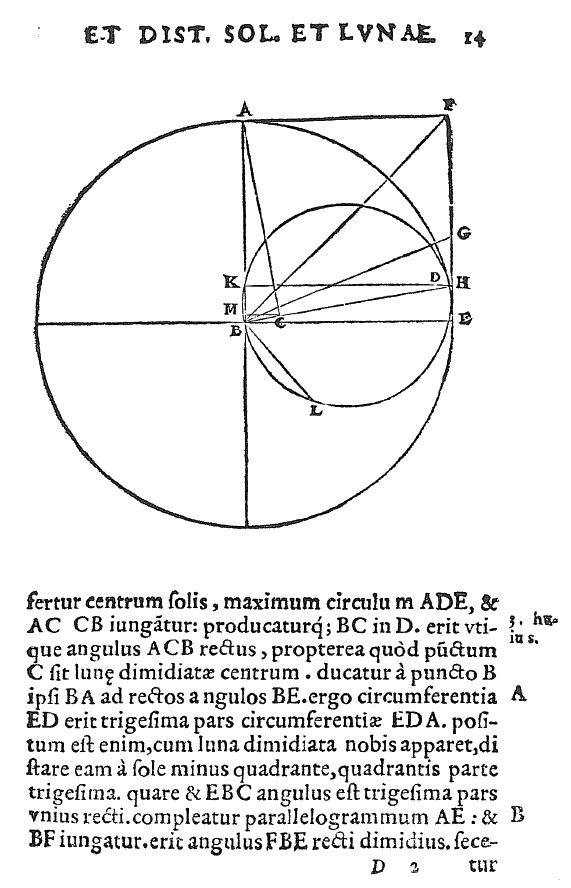
El llibre d’Aristarc, “Sobre els tamanys i les distàncies del sol i de la lluna”, traduit al llatí per Commandino l’any 1572, el teniu també en versió castellana. I aqui tenim una de les pàgines del llibre de Commandino. En notació traduida directament del grec, A representa el sol, B la terra i C la lluna: