Els objectes, quan giren, tenen un comportament estrany i poc intuïtiu. Encara que ens sembli rar, el que fa que puguem anar en bicicleta és el mateix que explica el comportament dels equinoccis o el que fa que una roda penjada no caigui.
Fixeu-fos en la imatge. Tenim una petita roda penjada d’un cordill per un dels extrems del seu eix. Però la roda, aquest giròscop, no cau. Enlloc de caure, gira lentament al voltant de la vertical del cordill que la suporta. En aquest video del MIT podeu veure un senzill experiment que ens ensenya el que passa. És estrany, oi? El comportament de la roda de bicicleta és exactament el mateix que el de la roda de la foto del principi d’aquest article. Sorprenentment, la roda de bicicleta no cau sinó que gira lentament al voltant de la corda que l’aguanta per un dels extrems de l’eix.
Sempre que feu girar molt de pressa una roda qualsevol i tot seguit la pengeu d’un dels extrems del seu eix, observareu el mateix efecte. Si la roda no girés, és evident que no es podria aguantar i que cauria. Però el seu gir ho canvia tot. Tots els objectes que giren ràpid reaccionen en una direcció inesperada. Per ser més precisos, reaccionen en direcció perpendicular a la que ens diu la nostra intuïció. Podríem dir que les rodes i els objectes que giren ràpid tenen un “comportament perpendicular“. La roda de bicicleta del vídeo i el nostre giròscop, en comptes de caure cap avall, es mouen parsimoniosament de manera horitzontal.
Estem acostumats a veure bicicletes. Però si pensem una mica, veurem que les bicicletes es mouen seguint aquest mateix comportament estrany. Les rodes de la bicicleta fan de giròscop. Amb la bicicleta en moviment, proveu de girar una mica el manillar a la dreta o a l’esquerra. Veureu que la bicicleta s’inclina de costat. És el mateix que passa en aquest vídeo: quan fem girar el giròscop a la dreta o a l’esquerra, s’inclina. Un cop més, reacciona en direcció perpendicular a l’esperada. Aprendre a anar en bicicleta és aprendre aquesta íntima connexió, aquesta dansa entre els moviments del manillar i les inclinacions laterals de la bicicleta.
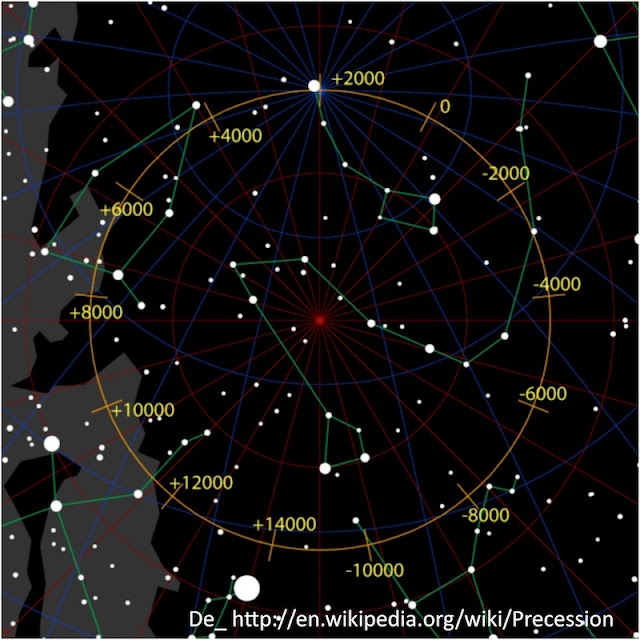
Si imagineu que fixeu un pal llarg i vertical a una bicicleta i penseu cóm aniria canviant la seva direcció quan la bicicleta avança, veuríeu que es mou com una baldufa. Les bicicletes i les baldufes segueixen les mateixes lleis de la física. A més de girar, el seu eix descriu un moviment lent, anomenat de precessió, al voltant de la vertical. El seu “comportament perpendicular” converteix la caiguda en aquest típic moviment de precessió de les baldufes. Fins i tot el nostre planeta, la Terra, té aquest mateix moviment de precessió. El nostre planeta no és esfèric, sinó que el seu major radi a la zona equatorial el converteix en una roda gegant. I com sabem, l’equador de la Terra forma un angle d’uns 23 graus amb el pla de la seva trajectòria. Les forces d’atracció del Sol i de la Lluna intenten portar l’equador de la terra cap al pla de l’eclíptica, el de la seva trajectòria. L’efecte, un cop més, apareix en direcció perpendicular. En comptes de redreçar-se, l’eix de la Terra fa un moviment lent de precessió al voltant de la perpendicular a l’eclíptica. El moviment de la Terra és exactament el mateix que el d’una baldufa, encara que molt més lent (la seva inèrcia és immensa). El moviment de precessió fa que el seu eix vagi canviant de direcció. Mireu la foto al final d’aquest article. Ens indica el punt on apunta l’eix de la Terra (la direcció del nord, el punt del cel al voltant del qual totes les estrelles giren cada nit), per tots els anys des d’el 10000 abans de Crist fins a l’any 14000. Ara, l’any 2012, la direcció del nord és la de l’Estrella Polar, amb molt bona aproximació. Però a l’època dels grecs, aquesta direcció era més propera a l’altre extrem de l’Óssa Menor. L’eix de la Terra dóna tota una volta de precessió cada 25780 anys. Com que 25780/360=71, la direcció del nord es mou un grau cada 71 anys i 7 mesos. La precessió de l’eix de la terra fa que es moguin el pla de l’equador i el punt Vernal (o punt d’Àries) que assenyala l’equinocci de primavera. A principis de l’era cristiana el Sol es projectava al començament de la primavera en la constel·lació d’Àries. Actualment ha girat i es projecta sobre la constel·lació dels Peixos.
Aquest fenomen de “comportament perpendicular” és conseqüència de la llei de la inèrcia. Galileu va ser el primer de parlar d’inèrcia, tot desmentint la teoria de l’impuls d’Aristòtil. Després, Isaac Newton la va formular i incorporar a les lleis fonamentals de la dinàmica: Tot objecte lliure de forces exteriors es manté en repòs o es desplaça amb moviment rectilini uniforme. El moviment uniforme i en línia recta és suau i no requereix cap força. I tots sabem que els canvis produeixen (i són produïts per) forces. Quan l’autobús en què viatgem frena bruscament, ens hem d’agafar per no caure endavant. Quan anem en cotxe i el conductor entra en una corba tancada, la força centrífuga ens prem contra la porta. El moviment en el autobús és rectilini però deixa de ser uniforme quan frena; en el cotxe, deixa de ser rectilini. En tots dos cassos, el nostre cos voldria continuar el seu moviment rectilini i uniforme. Per això notem una pressió contra la porta del cotxe: si s’obrís i no portéssim cinturó sortiríem disparats en línia recta com la pedra que surt de la fona. I quan l’autobús frena, no és pas que caiguem endavant. Un observador des d’el carrer veurà que el que es queda enrere és l’autobús que està frenant, mentre que el nostre cos intenta continuar, tot mantenint la velocitat prèvia a la frenada.
Observem un cop més la imatge del nostre giròscop penjat d’un cordill per un dels seus extrems. Totes les partícules de la roda giren ràpidament, i totes elles segueixen la llei de la inèrcia. De fet, si imagineu una roda feta d’un material poc atapeït, ben segur que la rotació la disgregaria per efecte de la força centrifuga. Pensem ara en el comportament de quatre d’aquestes partícules: la partícula A que és la que està passant pel punt superior de la roda, la B que és la que en aquest moment tenim més a prop, la C que està passant pel punt inferior i la D que es troba a la part posterior. En d’altres paraules, si mirem la roda des de l’esquerra de la foto, la partícula A és la que en aquest moment està passant per la posició de les 12 del rellotge, mentre que les partícules B, C i D són les que es troben a les 3, les 6 i les 9 respectivament. La velocitat de les partícules A i C és horitzontal i força gran, si el gir de la roda és prou ràpid. Encara que el giroscopi comenci a caure, amb un balanceig al voltant del punt on l’aguanta el cordill, la seva velocitat continuarà essent horitzontal. No en canvien ni la direcció ni la magnitud. Ho podeu comprovar si imagineu el giroscopi en dues posicions: en la de la foto i en una posició on hagi caigut lleugerament. Els punts A i C s’han mogut una mica de costat, però les seves velocitats continuen essent horitzontals, sense haver pràcticament canviat gens (cal tenir en compte que assumim que la velocitat horitzontal de A i C és elevada). Segons la llei de la inèrcia, els punts A i C no ofereixen resistència, per tant. En canvi, no passa pas el mateix amb les partícules B i D. Suposem que B s’està movent en sentit vertical i cap amunt. Llavors, D s’estarà movent amb la mateixa velocitat però cap avall (tot depèn del sentit de gir). Si el giroscopi comença a caure, estem obligant a canviar la direcció de les velocitats de les partícules B i D ja que estem inclinant la roda i aquestes dues velocitats sempre són tangents a la roda. La velocitat de B s’ha de torçar cap a l’esquerra (en la nostra imatge) mentre que la velocitat de D (que, recordem-ho, va cap avall) s’ha de torçar cap a la dreta. Estem obligant a girar els cotxes imaginaris en que es mouen les partícules B i D. Les partícules reaccionen, i així com nosaltres empenyem la porta del cotxe, les partícules B i D exerceixen cada una d’elles una força sobre el giroscopi. Ara bé, com que les velocitats de B i D són contràries, aquestes forces també són contràries: la partícula B empeny cap a la dreta de la foto a la vegada que la partícula D ho fa cap a l’esquerra. És com si volguéssim tancar una aixeta: premem cap a la dreta amb el dit índex i cap a l’esquerra amb el polze. El resum de tot plegat és que el giroscopi comença a girar al voltant de l’eix vertical del cordill que l’aguanta, enlloc de caure. Evidentment, el raonament complet és més complex perquè cal tenir en compte totes les partícules intermèdies, no només les quatre partícules A, B, C i D que hem considerat. L’explicació física de tots aquests fenòmens es basa en les lleis de conservació (i de variació) del moment angular, com podeu veure aquí.
Gràcies a aquest comportament estrany de les rodes i del nostre planeta, gràcies a la precessió, el cel de nit ens ofereix un extraordinari calendari secular. Quan estem a punt de fer 72 anys, el pol nord de l’esfera celeste (el centre del moviment aparent de rotació de les estrelles al llarg de la nit) s’ha desplaçat un grau des de la posició que tenia el dia del nostre naixement. Podem veure on era en temps de Plató o d’Arquímedes, i podem saber on serà d’aquí a vint o quaranta segles:
