Tinc un amic que, quan és de viatge, enyora el seu poble. Als vespres, quan cau la llum, ho intenta mitigar mentre mira el cel, cap a l’horitzó, en direcció a Cadaqués.

L’any passat va anar a Florència, i ho tenia fàcil. Només havia de mirar cap a l’oest. Però aquest any ha viatjat a Kyoto, al Japó. En quina direcció ha de mirar, als capvespres?

Sabem que la distància més curta entre dos punts és la línia recta. Però això, a la terra no és massa pràctic i no li serveix, al nostre amic. No vol mirar cap avall, cap als peus. Sabem que la terra és una quasi-esfera. I el camí més curt entre dos punts situats sobre una superfície, no és una recta. És una corba que s’anomena geodèsica.

Amb el grau d’aproximació que hem de treballar, podem perfectament suposar que la terra és una esfera. Doncs bé, si tenim dos punts situats sobre una esfera (en el nostre cas, Cadaqués i Kyoto) i aquests dos punts no són antípodes, la geometria ens diu que existeix un únic camí mínim entre ells. El nostre amic només ha d’esbrinar quin és aquest camí geodèsic, i ja ha resolt el problema d’on dirigir la seva mirada als vespres. Val a dir que si viatja a les antípodes, a Nova Zelanda, es trobarà en un punt singular. En aquest cas no hi ha una direcció de distància mínima, sinó que la distància és idèntica sigui quina sigui la direcció en què miri. A les antípodes pot mirar en qualsevol direcció, sempre estarà dirigint la mirada a Cadaqués…

Deixant a banda les antípodes, sabem que qualsevol parell de punts sobre la terra defineix una única corba geodèsica i una única direcció de camí mínim. Però, com podem determinar-la?

Dibuixar una línia recta al mapa no serveix, perquè la terra, com tota esfera, no té punts privilegiats. Per això no hi ha mapes perfectes, com bé ens va explicar Gerard Kremer (Mercator). Tot mapa és una projecció de la terra (o de part d’ella) sobre una superfície, habitualment un pla, cilindre o con. Però, a la terra, tots els punts són iguals i en canvi els mapes han de tenir un punt central. Els mapamundis aconsegueixen no deformar determinats punts de la terra, però deformen els altres. El resultat és que les geodèsiques, als mapes, no són línies rectes. I això ens complica els problema.

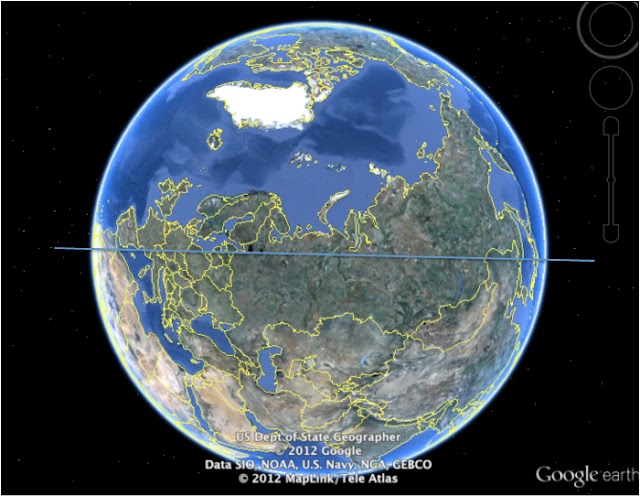
Una solució senzilla és treballar sobre un mapa que no deformi: un mapa en un globus terraqüi. Ho podem fer amb una bola del món o, més fàcilment, amb un geo-navegador com Google-Earth. Simplement anem girant el globus terraqüi fins aconseguir que la línia recta que uneix els nostres dos punts divideixi la terra en dues parts iguals. Llavors haurem trobat la única direcció des de la qual veiem els dos punts i l’arc de la seva geodèsica com un segment de recta que els uneix (veure nota al final).

Si ho fem amb Cadaqués i Kyoto, aconseguirem la imatge de la figura de sota. La geodèsica és un arc de cercle màxim, contingut en el pla que passa per Cadaqués, Kyoto i el centre de la terra. De fet, és com un nou equador, un equador que ens agermana amb els habitants de Kyoto. Podríem agafar un ganivet virtual i tallar la terra, com una síndria, en dues meitats idèntiques i amb els nostres dos punts en el pla de tall. Marqueu dos punts qualsevols a la superfície d’una síndria. Hi ha una única manera de tallar la síndria en dues parts iguals i fent que el tall passi pels dos punts marcats: és el tall que ens marca el camí geodèsic entre els dos punts.

El nostre amic, als capvespres, ha de mirar no pas cap a l’oest, sino cap al nord-oest, bastant més en direcció nord. La geodèsica en aquest cas passa prop de les regions polars.

 
Nota: La direcció des de la que veiem els dos punts i la seva geodèsica com un segment de recta, és la direcció de la suma dels dos vectors (A menys C) i (B menys C) on A i B són els nostres dos punts i C és el centre de la terra.